At first, we sample ![]() in the
in the ![]() (
(![]() is odd) equidistant points around
is odd) equidistant points around ![]() :
:
![]()
where ![]() is some step. Then we interpolate points
is some step. Then we interpolate points ![]() by polynomial
by polynomial
(1) 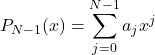
Its coefficients ![]() are found as a solution of system of linear equations:
are found as a solution of system of linear equations:
(2) ![]()
Here are references to existing equations: (1), (2). Here is reference to non-existing equation (??).